- Research Article
- Open access
- Published:
Budget Allocation in a Competitive Communication Spectrum Economy
EURASIP Journal on Advances in Signal Processing volume 2009, Article number: 963717 (2009)
Abstract
This study discusses how to adjust "monetary budget" to meet each user's physical power demand, or balance all individual utilities in a competitive "spectrum market" of a communication system. In the market, multiple users share a common frequency or tone band and each of them uses the budget to purchase its own transmit power spectra (taking others as given) in maximizing its Shannon utility or pay-off function that includes the effect of interferences. A market equilibrium is a budget allocation, price spectrum, and tone power distribution that independently and simultaneously maximizes each user's utility. The equilibrium conditions of the market are formulated and analyzed, and the existence of an equilibrium is proved. Computational results and comparisons between the competitive equilibrium and Nash equilibrium solutions are also presented, which show that the competitive market equilibrium solution often provides more efficient power distribution.
1. Introduction
The competitive economy equilibrium problem of a communication system consists of finding a set of prices and distributions of frequency or tone power spectra to users such that each user maximizes his/her utility, subject to his/her budget constraints, and the limited power bandwidth resource is efficiently utilized. Although the study of the competitive equilibrium can date back to Walras [1] work in 1874, the concepts applied to a communication system just emerged few years ago because of the great advances in communication technology recently. In a modern communication system such as cognitive radio or digital subscriber lines (DSL), users share the same frequency band and how to mitigate interference is a major design and management concern. The Frequency Division Multiple Access (FDMA) mechanism is a standard approach to eliminate interference by dividing the spectrum into multiple tones and preassigning them to the users on a nonoverlapping basis. However, this approach may lead to high system overhead and low bandwidth utilization. Therefore, how to optimize users' utilities without sacrificing the bandwidth utilization through spectrum management becomes an important issue. That is why the spectrum management problem has recently become a topic of intensive research in the signal processing and digital communication community.
From the optimization perspective, the problem can be formulated either as a noncooperative Nash game [2–5]; or as a cooperative utility maximization problem [6, 7]. Several algorithms were proposed to compute a Nash equilibrium solution (Iterative Waterfilling Algorithm (IWFA) [2, 4]; Linear Complementarity Problem (LCP) [3]) or globally optimal power allocations (Dual decomposition method, [8–10]) for the cooperative game. Due to the problem's nonconvex nature, these algorithms either lack global convergence or may converge to a poor spectrum sharing strategy. Moreover, the Nash equilibrium solution may not achieve social communication economic efficiency; and, on the other hand, an aggregate social utility (i.e., the sum of all users' utilities) maximization model may not simultaneously optimize each user's individual utility.
Recently, Ye [11] proposed a competitive economy equilibrium solution that may achieve both social economic efficiency and individual optimality in dynamic spectrum management. He proved that a competitive equilibrium always exists for the communication spectrum market with Shannon utility for spectrum users, and under a weak-interference condition the equilibrium can be computed in a polynomial time. In [11], Ye assumes that the budget is fixed, but this paper deals how adjusting the budget can further improve the social utility and/or meet each individual physical demand. This adds another level of resource control to improve spectrum utilization.
This study investigates how to allocate budget between users to meet each user's physical power demand or balance all individual utilities in the competitive communication spectrum economy. We prove what follows.
-
(1)
A competitive equilibrium that satisfies each user's physical power demand always exists for the communication spectrum market with Shannon utilities if the total power demand is less than or equal to the available total power supply.
-
(2)
A competitive equilibrium where all users have identical utility value always exists for the communication spectrum market with Shannon utilities.
Computational results and comparisons between the competitive equilibrium and Nash equilibrium solutions are also presented. The simulation results indicate that the competitive economy equilibrium solution provides more efficient power distribution to achieve a higher social utility in most cases. Besides, the competitive economy equilibrium solution can make more users to obtain higher individual utilities than the Nash equilibrium solution does in most cases. Moreover, the competitive economy equilibrium takes the power supply capacity of each channel into account, while the Nash equilibrium model assumes the supply unlimited where each user just needs to satisfy its power demand.
The remainder of this paper is organized as follows. The mathematical notations are illustrated in Section 2. Section 3 describes the competitive communication spectrum market considered in this study. Section 4 formulates two competitive equilibrium models that address budget allocation on satisfying power demands and budget allocation on balancing individual utilities. Section 5 demonstrates a toy example of two users and two channels. Section 6 describes how to solve the market equilibrium and presents the computational results. Finally, conclusions are made in the last section.
2. Mathematical Notations
First, a few mathematical notations. Let  denote the
denote the  -dimensional Euclidean space;
-dimensional Euclidean space;  denote the subset of
denote the subset of  where each coordinate is nonnegative.
where each coordinate is nonnegative.  and
and  denote the set of real numbers and the set of nonnegative real numbers, respectively.
denote the set of real numbers and the set of nonnegative real numbers, respectively.
Let  denote the set of ordered
denote the set of ordered  -tuples
-tuples  and let
and let  denote the set of ordered
denote the set of ordered  -tuples
-tuples  , where
, where  for
for  . For each
. For each  , suppose there is a real utility function
, suppose there is a real utility function  , defined over
, defined over  . Let
. Let  be a subset of
be a subset of  defining for each point
defining for each point  , then the sequence
, then the sequence  will be termed an abstract economy. Here
will be termed an abstract economy. Here  represents the feasible action set of agent
represents the feasible action set of agent  that is possibly restricted by the actions of others, such as the budget restraint that the cost of the goods chosen at current prices dose not exceed his income, and the prices and possibly some or all of the components of his income are determined by choices made by other agents. Similarly, utility function
that is possibly restricted by the actions of others, such as the budget restraint that the cost of the goods chosen at current prices dose not exceed his income, and the prices and possibly some or all of the components of his income are determined by choices made by other agents. Similarly, utility function  for agent
for agent  depends on his or her actions
depends on his or her actions  , as well as actions
, as well as actions  made by all other agents. Also, denote
made by all other agents. Also, denote  for a given
for a given  .
.
A function  is said to be concave if for any
is said to be concave if for any  and any
and any  , we have
, we have  ; and it is strictly concave if
; and it is strictly concave if  for
for  . It is monotone increasing if for any
. It is monotone increasing if for any  ,
,  implies that
implies that  .
.
3. Competitive Communication Spectrum Market
Let the multiuser communication system consist of  transmitter-receiver pairs sharing a common frequency band discretized by
transmitter-receiver pairs sharing a common frequency band discretized by  tones. For simplicity, we will call each of such transmitter-receiver pair a "User." Each user
tones. For simplicity, we will call each of such transmitter-receiver pair a "User." Each user  will be endowed a "monetary" budget
will be endowed a "monetary" budget  and use it to "purchase" powers,
and use it to "purchase" powers,  , across tones
, across tones  , from an open market so as to maximize its own utility
, from an open market so as to maximize its own utility  :
:

where  and
and  are power units purchased by all other users, and
are power units purchased by all other users, and  is the unit price for tone
is the unit price for tone  in the market.
in the market.
A commonly recognized utility for user  ,
,  , in communication is the Shannon utility [12]:
, in communication is the Shannon utility [12]:

where parameter  denotes the normalized background noise power for user
denotes the normalized background noise power for user  at tone
at tone  , and parameter
, and parameter  is the normalized crosstalk ratio from user
is the normalized crosstalk ratio from user  to user
to user  at tone
at tone  . Due to normalization we have
. Due to normalization we have  for all
for all  . Clearly,
. Clearly,  is a continuous concave and monotone increasing function in
is a continuous concave and monotone increasing function in  for every
for every  .
.
There are four types of agents in this market. The first-type agents are users. Each user aims to maximize its own utility under its budget constraint and the decisions by all other users. The second-type agent, "Producer or Provider," who installs power capacity supply  to the market from a convex and compact set
to the market from a convex and compact set  to maximize his or her utility. We assume that they are fixed as
to maximize his or her utility. We assume that they are fixed as  in this paper, and
in this paper, and  , that is, the total power demand is less than or equal to the available total power supply.
, that is, the total power demand is less than or equal to the available total power supply.
The third agent, "Market," sets tone power unit "price"  , which can be interpreted as a "preference or ranking" of tones
, which can be interpreted as a "preference or ranking" of tones  . For example,
. For example,  and
and  simply mean that users may use one unit of
simply mean that users may use one unit of  to trade for two units of
to trade for two units of  .
.
The fourth agent, "Budgeting," allocates "monetary" budget  to user
to user  from a bounded total budget, say
from a bounded total budget, say  .
.
Figure 1 illustrates the interaction among four types of agents in the proposed competitive spectrum market. Each user  determines its power allocation
determines its power allocation  under its budget
under its budget  , power spectra unit price density
, power spectra unit price density  and the decisions by all other users
and the decisions by all other users  . The producer installs power capacity spectra density
. The producer installs power capacity spectra density  based on power spectra unit price density
based on power spectra unit price density  to maximize his or her utility. The market sets power spectra unit price density
to maximize his or her utility. The market sets power spectra unit price density  based on tone power distribution
based on tone power distribution  and power capacity spectra density
and power capacity spectra density  to make market clear. The budgeting agent allocates budget
to make market clear. The budgeting agent allocates budget  to user
to user  from a bounded total budget according to tone power distribution
from a bounded total budget according to tone power distribution  for satisfying power demands or balancing individual utilities. In this study, we assume power capacity spectra density
for satisfying power demands or balancing individual utilities. In this study, we assume power capacity spectra density  is fixed. Therefore,
is fixed. Therefore,  is determined first in the system.
is determined first in the system.
4. Budget Allocation in Competitive Communication Spectrum Market
In this section, we discuss how to adjust "monetary" budget to satisfy each user's prespecified physical power demand or to balance all individual utilities in a competitive spectrum market.
4.1. Budget Allocation on Satisfying Individual Power Demands
The first question is whether or not the "Budgeting" agent can adjust "monetary budget" for each user to meet each user's desired total physical power demand  that may be composed from any tone combination. We give an affirmative answer in this section.
that may be composed from any tone combination. We give an affirmative answer in this section.
A competitive market equilibrium is a power distribution  such that
such that
-
(i)
(user optimality)
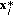 is a maximizer of (1) given
is a maximizer of (1) given 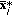 ,
,  and
and  for every
for every  ;
; -
(ii)
(market efficiency)
 ,
, 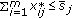 ,
,  for all
for all 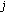 . This condition says that if tone power capacity
. This condition says that if tone power capacity  is greater than or equal to the total power consumption for tone
is greater than or equal to the total power consumption for tone 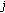 ,
, 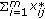 , then its equilibrium price
, then its equilibrium price 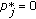 ;
; -
(iii)
(budgeting according to demands) given
 ,
, 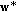 is a maximizer of
is a maximizer of 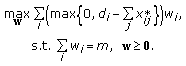 (3)
(3)This condition says that if user
 's power demand is not met, that is,
's power demand is not met, that is,  , then one should allocate more or all "money budget" to user
, then one should allocate more or all "money budget" to user  . Any budget allocation is optimal if
. Any budget allocation is optimal if 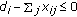 for all
for all  , that is, if every user's physical power demand is met.
, that is, if every user's physical power demand is met.
Since the "Budgeting" agent's problem is a bounded linear maximization, and all other agents' problems are identical to those in Ye [11], we have the following corollary.
Corollary 4.1.
The communication spectrum market with Shannon utilities has a competitive equilibrium that satisfies each user's tone power demand, if the total power demand is less than or equal to the available total power supply.
Now consider the KKT conditions of (1):

where  denotes any subgradient vector of
denotes any subgradient vector of  with respect to
with respect to  .
.
Since  and
and  , we have
, we have  and
and  . Then,
. Then,  . The optimality conditions in (4) can be simplified to
. The optimality conditions in (4) can be simplified to

The complete necessary and sufficient conditions for a competitive equilibrium with satisfied power demands can be summarized as

Note that the conditions  for all
for all  are implied by the conditions in (6): multiplying
are implied by the conditions in (6): multiplying  to both sides of the first inequality, we have
to both sides of the first inequality, we have  for all
for all  , which, together with other inequality conditions in (6), imply
, which, together with other inequality conditions in (6), imply

that is, every inequality in the sequence must be tight, which implies  for all
for all  .
.
On the other hand, the 4–6th conditions in (6) are optimality conditions of budget allocator's linear program, where  is the dual variable. Then, we have a characterization theorem of a competitive equilibrium that satisfies power demands.
is the dual variable. Then, we have a characterization theorem of a competitive equilibrium that satisfies power demands.
Theorem 4.2.
Every equilibrium of the discretized communication spectrum market with the Shannon utility that satisfies power demands has the following properties:
-
(1)
 (every tone power has a price);
(every tone power has a price); -
(2)
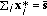 (all powers are allocated);
(all powers are allocated); -
(3)
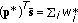 (all user budgets are spent);
(all user budgets are spent); -
(4)
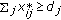 for all
for all  (all user demands are met);
(all user demands are met); -
(5)
If
 then
then 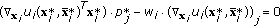 for all
for all  (every user only purchases most valuable tone power).
(every user only purchases most valuable tone power).
Proof.
Note that

Since  cannot be zero for all
cannot be zero for all  , there is at least one
, there is at least one  such that
such that

so that the first inequality of (6) implies that  .
.
The second property is from  ,
,  and
and  .
.
The third is from  for all
for all  and
and  .
.
We prove the fourth property by contradiction. Suppose,  for
for  for a nonempty index set
for a nonempty index set  . Then,
. Then,  for all
for all  so that
so that  for all
for all  . Then,
. Then,

which is a contradiction to the assumption  .
.
The last one is from the complementarity condition of user optimality.
The fourth property of Theorem 4.2 implies that equilibrium conditions (6) can be simplified to

Note that the constraint  is merely a normalizing constraint and it can be replaced by another type of normalizing constraint such as
is merely a normalizing constraint and it can be replaced by another type of normalizing constraint such as  . Moreover, multiple competitive equilibria may exist due to the nonconvexity of the optimality conditions of the spectrum management problem with minimal user power demands.
. Moreover, multiple competitive equilibria may exist due to the nonconvexity of the optimality conditions of the spectrum management problem with minimal user power demands.
4.2. Budget Allocation on Balancing Individual Utilities
The second question is whether or not the "Budgeting" agent can adjust "monetary budget" for each user such that a certain fairness is achieved in the spectrum market; for example, every user obtains the same utility value, which is also a critical issue in spectrum management. We again give an affirmative answer in this section.
Here, a competitive market equilibrium is a density point  such that
such that
-
(i)
(user optimality)
 is a maximizer of (1) given
is a maximizer of (1) given 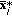 ,
,  and
and 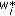 for every
for every  ;
; -
(ii)
(market efficiency)
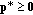 ,
, 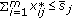 ,
, 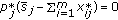 for all
for all 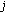 ;
; -
(iii)
(budgeting according to individual utilities) Given
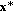 ,
, 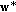 is a minimizer of
is a minimizer of 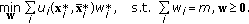 (12)
(12)This condition says that if user
 's utility is higher than any others', that is,
's utility is higher than any others', that is, 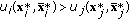 , then one should shift "money budget" from user
, then one should shift "money budget" from user  to user
to user 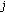 . Any budget allocation is optimal if
. Any budget allocation is optimal if  are identical for all
are identical for all  , that is, if every user has the same utility value.
, that is, if every user has the same utility value.
Since the "Budgeting" agent's problem is again a bounded linear maximization, and all other agents' problems are identical to those in Ye [11], we have the following corollary.
Corollary 4.3.
The communication spectrum market with Shannon utilities has a competitive equilibrium that balances each user's utility value.
The complete necessary and sufficient conditions for a competitive equilibrium with balanced utilities can be summarized as

Note that the conditions  for all
for all  are implied by the conditions in (13). On the other hand, the 4–6th conditions in (13) are optimality conditions of budget allocator's linear program for balancing utilities, where
are implied by the conditions in (13). On the other hand, the 4–6th conditions in (13) are optimality conditions of budget allocator's linear program for balancing utilities, where  is the dual variable.
is the dual variable.
Again, we have a characterization theorem of a competitive equilibrium that balances individual utilities.
Theorem 4.4.
Every equilibrium of the discretized communication spectrum market with the Shannon utility that balances individual utilities has the following properties:
(1) (every tone power has a price);
(every tone power has a price);
(2) (all powers are allocated);
(all powers are allocated);
(3) (all user budgets are spent);
(all user budgets are spent);
(4) are identical for all
are identical for all  (all user utilities are the same);
(all user utilities are the same);
-
(5)
If
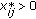 then
then 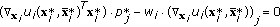 for all
for all 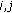 (every user only purchases most valuable tone power).
(every user only purchases most valuable tone power).
Proof.
The proof of properties 1, 2, 3, and 5 are the same as Theorem 4.2. The fourth property is from the 5th condition of (13). If  , then the user cannot participate the game. Therefore,
, then the user cannot participate the game. Therefore,  and
and  by the 5th condition of (13), which implies all user utilities are identical.
by the 5th condition of (13), which implies all user utilities are identical.
The fourth property of Theorem 4.4 implies that equilibrium conditions (13) can be simplified to

5. An Illustration Example
Consider two channels  and
and  , and two users
, and two users  and
and  . Let the Shannon utility function for user
. Let the Shannon utility function for user  be
be

and one for user  be
be

and let the aggregate social utility be the sum of the two individual user utilities.
Assume a competitive spectrum market with power supply for two channels is  and the initial endowments for two users is
and the initial endowments for two users is  . Then the competitive solution is
. Then the competitive solution is

where the utility of user  is 0.3522, the utility of user
is 0.3522, the utility of user  is 0.2139, and the social utility has value 0.5661.
is 0.2139, and the social utility has value 0.5661.
Now consider each of them has a physical power demand  . From above example we find
. From above example we find  can not satisfy user
can not satisfy user  's power demand
's power demand  if
if  . By the proposed method, we can adjust the initial budget endowments to
. By the proposed method, we can adjust the initial budget endowments to  and
and  , then the equilibrium price will remain the same and the equilibrium allocation will be
, then the equilibrium price will remain the same and the equilibrium allocation will be

where the utility of user  is 0.4771, the utility of user
is 0.4771, the utility of user  is 0.1761, and the social utility has value 0.6532.
is 0.1761, and the social utility has value 0.6532.
Since the Nash equilibrium model only considers each user's power demand, we set the power constraints of user  and user
and user  as 2 and get a Nash equilibrium
as 2 and get a Nash equilibrium  ,
,  ,
,  ,
,  , where the utility of user
, where the utility of user  is 0.3010, the utility of user
is 0.3010, the utility of user  is 0.1938, and the social utility has value
is 0.1938, and the social utility has value  . Since the power resource supply of each channel is assumed to be unconstrained in the Nash model, we see that Channel
. Since the power resource supply of each channel is assumed to be unconstrained in the Nash model, we see that Channel  supplies
supplies  units power and Channel
units power and Channel  supplies
supplies  . Even though, comparing the competitive equilibrium and Nash equilibrium solutions, one can see that the competitive equilibrium provides a power distribution that not only meets physical power demand and supply constraints but also achieves a much higher social utility than the Nash equilibrium does.
. Even though, comparing the competitive equilibrium and Nash equilibrium solutions, one can see that the competitive equilibrium provides a power distribution that not only meets physical power demand and supply constraints but also achieves a much higher social utility than the Nash equilibrium does.
Now consider user  and user
and user  need to have more balanced individual utilities. By the proposed method, we can adjust the initial endowments to
need to have more balanced individual utilities. By the proposed method, we can adjust the initial endowments to  and
and  , then the equilibrium price will remain the same and the equilibrium power distribution will be
, then the equilibrium price will remain the same and the equilibrium power distribution will be

where the utilities of user  and user
and user  are both
are both  , and the social utility is
, and the social utility is  .
.
If the power constraints of user  and user
and user  are set as
are set as  and
and  , respectively, then the Nash equilibrium will be
, respectively, then the Nash equilibrium will be  ,
,  ,
,  ,
,  , where the utility of user
, where the utility of user  is 0.1761, the utility of user
is 0.1761, the utility of user  is 0.2730, and the social utility has value
is 0.2730, and the social utility has value  . Comparing the competitive equilibrium and Nash equilibrium solutions again, one can see that the competitive equilibrium provides a power distribution that not only makes both users with an identical utility value but also achieves a higher social utility than the Nash equilibrium does.
. Comparing the competitive equilibrium and Nash equilibrium solutions again, one can see that the competitive equilibrium provides a power distribution that not only makes both users with an identical utility value but also achieves a higher social utility than the Nash equilibrium does.
6. Numerical Simulations
This section presents some computer simulation results on using two different approaches to achieve budget allocation for satisfying each user's power demand or balancing individual utilities. We compare the competitive equilibrium solution with Nash equilibrium solution in social utility and individual utilities under various number of channels and number of users in a weak-interference communication environment. In a weak-interference communication channel, the Shannon utility function is approximated by

where  represent the average of normalized crosstalk ratios for
represent the average of normalized crosstalk ratios for  . Furthermore, we assume
. Furthermore, we assume  , that is, the average cross-interference ratio is not above
, that is, the average cross-interference ratio is not above  or it is less than the self-interference ratio (always normalized to
or it is less than the self-interference ratio (always normalized to  ). In all simulated cases, the channel background noise levels
). In all simulated cases, the channel background noise levels  are chosen randomly from the interval
are chosen randomly from the interval  , and the normalized crosstalk ratios
, and the normalized crosstalk ratios  are chosen randomly from the interval [0, 1]. The power supply of each channel
are chosen randomly from the interval [0, 1]. The power supply of each channel  is
is  . The total budget is
. The total budget is  . All simulations are run on a Genuine Intel CPU 1.66 GHz Notebook.
. All simulations are run on a Genuine Intel CPU 1.66 GHz Notebook.
6.1. Budget Allocation on Satisfying Individual Power Demands
In this section, we compute the budget allocation where the competitive equilibrium meets power demands  or
or  for all users under various number of channels and number of users. Two approaches are adopted to find out the budget allocation strategy: one is solving the entire optimality conditions in (11) by optimization solver LINGO; the other is iteratively adjusting total budget
for all users under various number of channels and number of users. Two approaches are adopted to find out the budget allocation strategy: one is solving the entire optimality conditions in (11) by optimization solver LINGO; the other is iteratively adjusting total budget  among different users based on whether their power demands are satisfied or not. In the iterative algorithm, all user budgets
among different users based on whether their power demands are satisfied or not. In the iterative algorithm, all user budgets  are set as 1 initially, then the competitive equilibrium can be derived from given channel capacity and user budget. If some user's power demand is not satisfied in the resulting competitive equilibrium, the budgeting agent reallocates budget to users and computes a new competitive equilibrium. The procedure reiterates until a desired competitive equilibrium is reached for satisfying power demands. The iterative algorithm that allocates more budget to the users with more power shortage and keeps the total budget as
are set as 1 initially, then the competitive equilibrium can be derived from given channel capacity and user budget. If some user's power demand is not satisfied in the resulting competitive equilibrium, the budgeting agent reallocates budget to users and computes a new competitive equilibrium. The procedure reiterates until a desired competitive equilibrium is reached for satisfying power demands. The iterative algorithm that allocates more budget to the users with more power shortage and keeps the total budget as  is summarized in Algorithm 1.
is summarized in Algorithm 1.
Algorithm 1
Iterative algorithm for budget allocation on satisfying power demands
-
Step 1: Set power supply of each channel
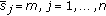 .
. -
Step 2: Initialize budget assigned to each user
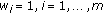 .
. -
Step 3: Loop:
-
(i)
Compute competitive economy equilibrium
 under
under 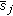 ,
, 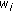
according to the model in [11].
-
(ii)
Obtain total allocated power for each user
 ,
,  .
. -
(iii)
Calculate average power shortage,
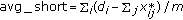 ,
,and minimal user budget,
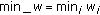 .
. -
(iv)
Update
 .
.Until
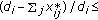 error tolerance,
error tolerance, 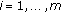 .
.
-
(i)
In each iteration, given channel capacity  and user budget
and user budget  , the competitive equilibrium is derived by an iterative waterfilling method [13]. Since the competitive equilibrium in each iteration satisfies
, the competitive equilibrium is derived by an iterative waterfilling method [13]. Since the competitive equilibrium in each iteration satisfies  and
and  , and each user optimizes his own utility under his budget constraint and the equilibrium prices, relatively increasing one user's budget makes him obtain more powers and others obtain fewer powers. In Algorithm 1, the user budget is reassigned according to the power shortage of each user in the equilibrium solution. The idea of comparing the user's power shortage with average shortage makes more budget be allocated to the users with higher power shortage and the total budget remains
, and each user optimizes his own utility under his budget constraint and the equilibrium prices, relatively increasing one user's budget makes him obtain more powers and others obtain fewer powers. In Algorithm 1, the user budget is reassigned according to the power shortage of each user in the equilibrium solution. The idea of comparing the user's power shortage with average shortage makes more budget be allocated to the users with higher power shortage and the total budget remains  . The term
. The term  aims to keep new
aims to keep new  not less than 0. The power demand value and the error tolerance have a significant impact on the number of iterations required to converge to the budget allocation where the competitive equilibrium meets the power demands. Figure 2 indicates the convergence behavior of the iterative algorithm for satisfying power demands for the case of 2 users and 2 channels illustrated in Section 5. Each user has a physical power demand
not less than 0. The power demand value and the error tolerance have a significant impact on the number of iterations required to converge to the budget allocation where the competitive equilibrium meets the power demands. Figure 2 indicates the convergence behavior of the iterative algorithm for satisfying power demands for the case of 2 users and 2 channels illustrated in Section 5. Each user has a physical power demand  . The error tolerance is set as 0.01. As the figure shows, at first, user
. The error tolerance is set as 0.01. As the figure shows, at first, user  has power shortage and user
has power shortage and user  has power surplus, then the algorithm converges after eight iterations and the errors
has power surplus, then the algorithm converges after eight iterations and the errors  for user
for user  and user
and user  are both below error tolerance 0.01.
are both below error tolerance 0.01.
Table 1 lists the number of iterations required to find out the budget allocation with  and
and  by the above iterative algorithm. The cases of
by the above iterative algorithm. The cases of  need more iterations since the total power demand
need more iterations since the total power demand  is equal to the total channel capacity
is equal to the total channel capacity  . This requirement is tight and the budget allocation makes each user get the same physical power in the competitive equilibrium, that is,
. This requirement is tight and the budget allocation makes each user get the same physical power in the competitive equilibrium, that is,  . Table 2 compares the CPU time used by two different approaches under power demands
. Table 2 compares the CPU time used by two different approaches under power demands  . The iterative algorithm spends much less time than the method of solving entire optimal conditions on finding out the budget allocation and the competitive equilibrium. We can also use the iterative method to solve large scale problems. The number of iterations and the CPU time required to solve large-scale problems are listed in Table 3. We observe that more iterations and CPU time spending for 100 users and 256 channels than those spending for 100 users and 1024 channels because the stop condition of the iterative algorithm is "
. The iterative algorithm spends much less time than the method of solving entire optimal conditions on finding out the budget allocation and the competitive equilibrium. We can also use the iterative method to solve large scale problems. The number of iterations and the CPU time required to solve large-scale problems are listed in Table 3. We observe that more iterations and CPU time spending for 100 users and 256 channels than those spending for 100 users and 1024 channels because the stop condition of the iterative algorithm is " error tolerance." In our simulations in Table 3,
error tolerance." In our simulations in Table 3,  for 100 users and 256 channels and
for 100 users and 256 channels and  for 100 users and 1024 channels, therefore the case of 100 users and 1024 channels requires fewer iterations and less total CPU time to reach the error tolerance 0.05 than the case of 100 users and 256 channels does. However the CPU time spending for one iteration in the case of 100 users and 256 channels is less than that in the case of 100 users and 1024 channels.
for 100 users and 1024 channels, therefore the case of 100 users and 1024 channels requires fewer iterations and less total CPU time to reach the error tolerance 0.05 than the case of 100 users and 256 channels does. However the CPU time spending for one iteration in the case of 100 users and 256 channels is less than that in the case of 100 users and 1024 channels.
 and
and  by the iterative algorithm, error tolerance = 0.01, average of 10 simulation runs.
by the iterative algorithm, error tolerance = 0.01, average of 10 simulation runs. between two approaches, error tolerance = 0.01 and average of 10 simulation runs.
between two approaches, error tolerance = 0.01 and average of 10 simulation runs. in large-scale problems by the iterative method, error tolerance = 0.05 and average of 10 simulation runs.
in large-scale problems by the iterative method, error tolerance = 0.05 and average of 10 simulation runs.In comparing competitive equilibrium with Nash equilibrium, the total power allocated to user  ,
,  , in competitive equilibrium is used as the power constraint for user
, in competitive equilibrium is used as the power constraint for user  in Nash equilibrium model to derive a Nash equilibrium. The simulation results averaged over 100 independent runs indicates that the average social utility of competitive equilibrium is higher than that of Nash equilibrium in all cases with
in Nash equilibrium model to derive a Nash equilibrium. The simulation results averaged over 100 independent runs indicates that the average social utility of competitive equilibrium is higher than that of Nash equilibrium in all cases with  and in most cases with
and in most cases with  , even though the difference is not significant. However, in certain type of problems, for instance, the channels being divided into two categories: high quality and low quality, the competitive equilibrium solution performs much better than the Nash equilibrium solution does. Table 4 compares social utility and individual utility between the competitive equilibrium and the Nash equilibrium when one half of channels with
, even though the difference is not significant. However, in certain type of problems, for instance, the channels being divided into two categories: high quality and low quality, the competitive equilibrium solution performs much better than the Nash equilibrium solution does. Table 4 compares social utility and individual utility between the competitive equilibrium and the Nash equilibrium when one half of channels with  chosen randomly from the interval
chosen randomly from the interval  and the other half of channels with
and the other half of channels with  chosen randomly from the interval
chosen randomly from the interval  . One can see that the competitive equilibrium significantly outperforms the Nash equilibrium in the social utility value and a much higher portion of users obtain higher individual utilities in the competitive equilibrium than those in the Nash equilibrium.
. One can see that the competitive equilibrium significantly outperforms the Nash equilibrium in the social utility value and a much higher portion of users obtain higher individual utilities in the competitive equilibrium than those in the Nash equilibrium.
 and Nash equilibrium(NE), error tolerance = 0.01 and average of 100 simulation runs.
and Nash equilibrium(NE), error tolerance = 0.01 and average of 100 simulation runs.6.2. Budget Allocation on Balancing Individual Utilities
To consider fairness, we adjust each user's endowed monetary budget  to reach a competitive equilibrium where the individual utilities are balanced. Herein we also adopt two approaches to find out the budget allocation: one is solving the entire optimality conditions in (14) by optimization solver LINGO; the other is iteratively adjusting total budget
to reach a competitive equilibrium where the individual utilities are balanced. Herein we also adopt two approaches to find out the budget allocation: one is solving the entire optimality conditions in (14) by optimization solver LINGO; the other is iteratively adjusting total budget  among different users based on their individual utilities.The iterative algorithm that shifts some budget from high-utility users to low-utility users and keeps the total budget as
among different users based on their individual utilities.The iterative algorithm that shifts some budget from high-utility users to low-utility users and keeps the total budget as  is summarized in Algorithm 2.
is summarized in Algorithm 2.
Algorithm 2
Iterative algorithm for budget allocation on balancing individual utilities
-
Step 1: Set power supply of each channel
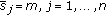 .
. -
Step 2: Initialize budget assigned to each user
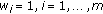 .
. -
Step 3: Loop:
-
(i)
Compute competitive economy equilibrium
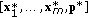 under
under  ,
, 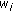
according to the model in [11].
-
(ii)
Obtain individual utility of each user
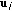 .
. -
(iii)
Calculate average reciprocal of individual utility,
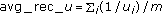 ,
,and minimal user budget,
 .
. -
(iv)
Update
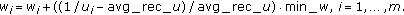
Until
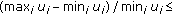 difference tolerance.
difference tolerance.
-
(i)
Algorithm 2 is similar to Algorithm 1 for budget allocation on satisfying power demands. For balancing individual utilities, herein the user budget is adjusted based on the individual utility in the equilibrium solution. The idea of using the reciprocal of individual utility makes some budget be transferred from the high-utility users to low-utility users. Since relatively increasing one user's budget makes him obtain more powers and others obtain fewer powers, this will decrease the difference between highest individual utility and lowest individual utility. The term  aims to keep new
aims to keep new  not less than 0. The difference tolerance significantly affects the number of iterations required to converge to the budget allocation. Figure 3 indicates the convergence behavior of the iterative algorithm for balancing individual utilities for the case of 2 users and 2 channels illustrated in Section 5. The difference tolerance is set as 0.01. As the figure shows, at first, the difference
not less than 0. The difference tolerance significantly affects the number of iterations required to converge to the budget allocation. Figure 3 indicates the convergence behavior of the iterative algorithm for balancing individual utilities for the case of 2 users and 2 channels illustrated in Section 5. The difference tolerance is set as 0.01. As the figure shows, at first, the difference  is higher than 0.6, then the algorithm converges after eighteen iterations and the difference is below difference tolerance 0.01.
is higher than 0.6, then the algorithm converges after eighteen iterations and the difference is below difference tolerance 0.01.
Table 5 lists the number of iterations required to converge to the budget allocation for balancing individual utilities by the iterative algorithm. Table 6 compares the CPU time used by two different approaches to achieve the budget allocation. The iterative algorithm spends less CPU time than the method of solving the entire optimal conditions. Treating the budget allocation problem by solving the entire optimal conditions can obtain a budget allocation where the competitive equilibrium has exactly identical individual utility value for each user. Table 7 lists the number of iterations and the CPU time required to solve large-scale problems for balancing utilities by the iterative method. We observe that more iterations are required for 100 users and 256 channels than those required for 100 users and 1024 channels because the stop condition of the proposed algorithm is " difference tolerance." In our simulations in Table 7, the balanced individual utilities for 100 users and 1024 channels are higher than those for 100 users and 256 channels, therefore the case of 100 users and 1024 channels requires fewer iterations to reach the difference tolerance 0.05 than the case of 100 users and 256 channels does. However the CPU time spending for one iteration in the case of 100 users and 256 channels is less than that in the case of 100 users and 1024 channels.
difference tolerance." In our simulations in Table 7, the balanced individual utilities for 100 users and 1024 channels are higher than those for 100 users and 256 channels, therefore the case of 100 users and 1024 channels requires fewer iterations to reach the difference tolerance 0.05 than the case of 100 users and 256 channels does. However the CPU time spending for one iteration in the case of 100 users and 256 channels is less than that in the case of 100 users and 1024 channels.
In comparing competitive equilibrium with Nash equilibrium, the total power allocated to each user in competitive equilibrium is also used as the power constraint to derive a Nash equilibrium. The simulation results averaged over 100 independent runs are displayed in Table 8. We find that, in most cases, more users get higher individual utilities in competitive equilibrium than those in Nash equilibrium and the social utility of competitive equilibrium remains higher than that of Nash equilibrium. Table 9 lists the comparisons in the communication environment involving two tiers of channels, one half of channels with  chosen randomly from the interval
chosen randomly from the interval  and the other half of channels with
and the other half of channels with  chosen randomly from the interval
chosen randomly from the interval  . We can observe that the competitive equilibrium not only makes more users obtain higher individual utilities but also significantly enhances the social utility. In other words, using budget allocation we can derive a competitive equilibrium that provides a power allocation strategy to balance individual utilities without sacrificing the social utility. Moreover, in the competitive equilibrium model with balanced individual utilities, all users have identical utility value. However, in the Nash equilibrium model the average difference between maximal individual utility and minimal individual utility is over
. We can observe that the competitive equilibrium not only makes more users obtain higher individual utilities but also significantly enhances the social utility. In other words, using budget allocation we can derive a competitive equilibrium that provides a power allocation strategy to balance individual utilities without sacrificing the social utility. Moreover, in the competitive equilibrium model with balanced individual utilities, all users have identical utility value. However, in the Nash equilibrium model the average difference between maximal individual utility and minimal individual utility is over  .
.
7. Conclusions
This study proposes two competitive equilibrium models: (1) to satisfy each user's physical power demand and (2) to balance all individual utilities in a competitive communication spectrum economy. Theoretically, we prove that a competitive equilibrium with physical power demand requirements always exists for the communication spectrum market with Shannon utility if the total power demand is less than or equal to the available total power supply. A competitive equilibrium with identical individual utilities also exists for the communication spectrum market with Shannon utility. Computationally, we use two approaches to find out the budget allocation where the competitive equilibrium satisfies power demand or balances individual utilities: one solves the characteristic equilibrium conditions and the other employs an iterative tatonament-type method by adjusting budget to each user. The iterative method performs significantly faster and can efficiently solve large-scale problems, which makes the competitive economy equilibrium model applicable in real-time spectrum management.
In comparing with the Nash equilibrium solution under the identical power usage of each user obtained from the competitive equilibrium model, our computational results show that the social utility of the competitive equilibrium solution is better than that of the Nash equilibrium solution in most cases. Under the equilibrium condition with balanced individual utilities, the competitive economy equilibrium solution makes more users obtain higher individual utilities than Nash equilibrium solution does without sacrificing the social utility.
In this study, we propose a centralized algorithm to reach a desired competitive equilibrium for satisfying power demands or balancing individual utilities. In the future, a distributed algorithm should be developed especially when a centralized controller is not available in the network. Besides, although the iterative method works well in our computational experiments, its convergence is unproven. We plan to do so in future work. We would also consider further study in how to adjust another exogenous factor  (power supply) to achieve a better social solution while maintaining individual satisfaction. That is, how to set the power supply capacity for each channel to make spectrum power allocation more efficient under the competitive equilibrium market model.
(power supply) to achieve a better social solution while maintaining individual satisfaction. That is, how to set the power supply capacity for each channel to make spectrum power allocation more efficient under the competitive equilibrium market model.
References
Walras L: Elements of Pure Economics, or the Theory of Social Wealth. Porcupine Press, Paris, France; 1874.
Chung ST, Kim SJ, Lee J, Cioffi JM: A game-theoretic approach to power allocation in frequency-selective Gaussian interference channels. Proceedings of IEEE International Symposium on Information Theory (ISIT '03), June-July 2003, Yokohama, Japan 316.
Luo Z-Q, Pang J-S: Analysis of iterative waterfilling algorithm for multiuser power control in digital subscriber lines. EURASIP Journal on Applied Signal Processing 2006, 2006:-10.
Yu W, Ginis G, Cioffi JM: Distributed multiuser power control for digital subscriber lines. IEEE Journal on Selected Areas in Communications 2002,20(5):1105-1115. 10.1109/JSAC.2002.1007390
Yamashita N, Luo Z-Q: A nonlinear complementarity approach to multiuser power control for digital subscriber lines. Optimization Methods & Software 2004,19(5):633-652. 10.1080/1055678042000218975
Cendrillon R, Yu W, Moonen M, Verlinden J, Bostoen T: Optimal multiuser spectrum balancing for digital subscriber lines. IEEE Transactions on Communications 2006,54(5):922-933.
Yu W, Lui R, Cendrillon R: Dual optimization methods for multiuser orthogonal frequency division multiplex systems. Proceedings of IEEE Global Telecommunications Conference (GLOBECOM '04), November-December 2004, Dallas, Tex, USA 1: 225-229.
Chan VMK, Yu W: Joint multiuser detection and optimal spectrum balancing for digital subscriber lines. EURASIP Journal on Applied Signal Processing 2006, 2006:-13.
Lui R, Yu W: Low-complexity near-optimal spectrum balancing for digital subscriber lines. Proceedings of IEEE International Conference on Communications (ICC '05), May 2005, Seoul, Korea 3: 1947-1951.
Yu W, Lui R: Dual methods for nonconvex spectrum optimization of multicarrier systems. IEEE Transactions on Communications 2006,54(7):1310-1322.
Ye Y: Competitive communication spectrum economy and equilibrium. In working paper. Stanford University, Stanford, Calif, USA; October 2007.
Cover TM, Thomas JA: Elements of Information Theory. John Wiley & Sons, New York, NY, USA; 1991.
Xie Y, Armbruster B, Ye Y: Dynamic spectrum management with the competitive market model. In working paper. Stanford University, Stanford, Calif, USA; February 2009.
Acknowledgments
This research is supported in part by Taiwan NSC Grants NSC-095-SAF-I-564-635-TMS, NSC 96-2416-H-158-003-MY3, and the Fulbright Scholar Program. The research also is supported in part by Taiwan NSC Grants NSC-095-SAF-I-564-640-TMS, NSC 96-2416-H-027-004-MY3, and the Fulbright Scholar Program, and supported in part by NSF DMS-0604513.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Lin, MH., Tsai, JF. & Ye, Y. Budget Allocation in a Competitive Communication Spectrum Economy. EURASIP J. Adv. Signal Process. 2009, 963717 (2009). https://doi.org/10.1155/2009/963717
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/963717

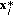 is a maximizer of (1) given
is a maximizer of (1) given 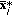 ,
,  and
and  for every
for every  ;
; ,
, 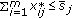 ,
,  for all
for all 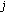 . This condition says that if tone power capacity
. This condition says that if tone power capacity  is greater than or equal to the total power consumption for tone
is greater than or equal to the total power consumption for tone 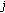 ,
, 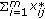 , then its equilibrium price
, then its equilibrium price 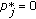 ;
;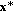 ,
, 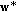 is a maximizer of
is a maximizer of 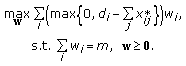
 's power demand is not met, that is,
's power demand is not met, that is,  , then one should allocate more or all "money budget" to user
, then one should allocate more or all "money budget" to user  . Any budget allocation is optimal if
. Any budget allocation is optimal if 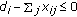 for all
for all  , that is, if every user's physical power demand is met.
, that is, if every user's physical power demand is met. (every tone power has a price);
(every tone power has a price);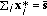 (all powers are allocated);
(all powers are allocated);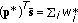 (all user budgets are spent);
(all user budgets are spent);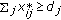 for all
for all  (all user demands are met);
(all user demands are met); then
then 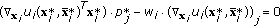 for all
for all  (every user only purchases most valuable tone power).
(every user only purchases most valuable tone power). is a maximizer of (1) given
is a maximizer of (1) given 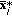 ,
,  and
and 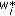 for every
for every  ;
;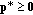 ,
, 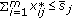 ,
, 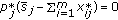 for all
for all 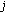 ;
;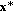 ,
, 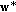 is a minimizer of
is a minimizer of 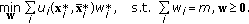
 's utility is higher than any others', that is,
's utility is higher than any others', that is, 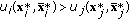 , then one should shift "money budget" from user
, then one should shift "money budget" from user  to user
to user 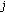 . Any budget allocation is optimal if
. Any budget allocation is optimal if  are identical for all
are identical for all  , that is, if every user has the same utility value.
, that is, if every user has the same utility value.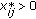 then
then 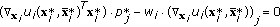 for all
for all 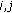 (every user only purchases most valuable tone power).
(every user only purchases most valuable tone power).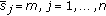 .
.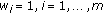 .
. under
under 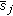 ,
, 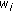
 ,
,  .
.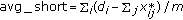 ,
,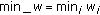 .
. .
.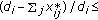 error tolerance,
error tolerance, 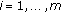 .
.
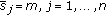 .
.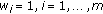 .
.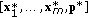 under
under  ,
, 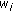
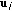 .
.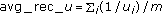 ,
, .
.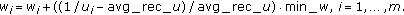
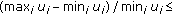 difference tolerance.
difference tolerance.